fonksiyon4

G. BİLEŞKE FONKSİYON

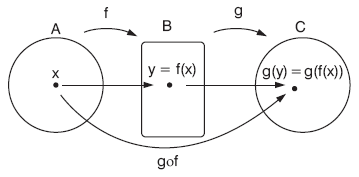
f : A ® B, g : B ® C fonksiyonları tanımlansın.

f ve g yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f nin bileşke fonksiyonu denir.

Buna göre,

f : A ® B ve g : B ® C olmak üzere, gof : A ® C fonksiyonuna f ile g nin bileşke fonksiyonu denir ve g bileşke f diye okunur.

(gof)(x) = g[f(x)] tir.

Bileşke işleminin değişme özeliği yoktur. Bu durumda, fog ¹ gof dir. Bazı fonksiyonlar için fog = gof olabilir. Ancak bu “fonksiyonlarda değişme özeliği yoktur.” gerçeğini değiştirmez.

	Fonksiyonlarda bileşke işleminin birleşme özeliği vardır. Bu durumda (fog)oh = fo(goh) = fogoh olur.
	I birim fonksiyon olmak üzere, foI = Iof = f ve f–1of = fof–1 = I dır.
	f, g ve h fonksiyonları bire bir ve örten olmak üzere, (fog)–1 = g–1of–1 ve (fogoh)–1 = h–1og–1of–1 dir.
	(fog)(x) = h(x) ise, f(x) = (hog–1)(x) dir. ise, g(x) = (f–1oh)(x) tir.

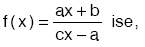
•  f–1 (x) = f(x) tir. •  (fof) (x) = x •  (fofof) (x) = f(x) •  (fofofof) (x) = x

H. FONKSİYONUN GRAFİĞİ

Bir fonksiyonun elemanlarına analitik düzlemde karşılık gelen noktaların kümesine bu fonksiyonun grafiği denir.

f : A ® B, f = {(x, y)|x Î A, y Î B, y = f(x)}

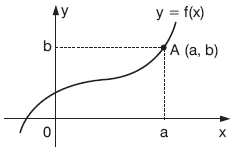(a, b) Î f olduğundan f(a) = b dir. Ayrıca, f–1(b) = a dır.

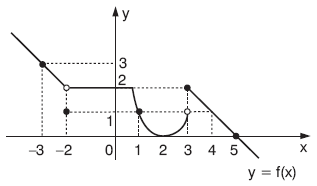
Yukarıdaki y = f(x) fonksiyonunun grafiğine göre, f(–3) = 3, f(–2) = 1, f(–1) = 2, f(0) = 2, f(1) = 1, f(2) = 0, f(3) = 2, f(4) = 1, f(5) = 0 dır.

 Çıkmış sorular için tıklayınız