fonksiyon 2

C. FONKSİYON ÇEŞİTLERİ

1. Bire Bir Fonksiyon

Bir fonksiyonda farklı elemanların görüntüleri de farklıysa fonksiyon bire birdir..

BBuna göre, bire bir fonksiyonda,

“x₁, x₂ Î A için, x₁ ¹ x₂ iken f(x₁) ¹ f(x₂) olur.

Diğer bir ifadeyle,

“x₁, x₂ Î A için, f(x₁) = f(x₂) iken

x₁ = x₂ ise, f  fonksiyonu bire birdir.

Ü	s(A) = m ve s(B) = n (n ³ m) olmak üzere, A dan B ye tanımlanabilecek bire bir fonksiyonların sayısı,

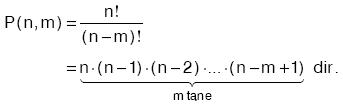2. Örten Fonksiyon

Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir.

Ü	f : A ® B f(A) = B ise, f örtendir.
Ü	s(A) = m olmak üzere, A dan A ya tanımlanabilen bire bir örten fonksiyonların sayısı, m! = m × (m – 1) × (m – 2) × … × 3 × 2 × 1 dir.

3. İçine Fonksiyon

Örten olmayan fonksiyona içine fonksiyon denir.

Ü	İçine fonksiyonun değer kümesinde eşlenmemiş eleman vardır.
Ü	s(A) = m olmak üzere, A dan A ya tanımlanabilen içine fonksiyonların sayısı mm – m! dir.

4. Birim (Etkisiz) Fonksiyon

Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.

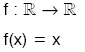
ise, f birim (etkisiz) fonksiyondur.

Birim fonksiyon genellikle I ile gösterilir.

5. Sabit Fonksiyon

Tanım kümesindeki bütün elemanları değer küme-sindeki bir elemana eşleyen fonksiyonasabit fonksiyon denir.

	“x Î A ve c Î B için, f : A ® B f(x) = c ise, f sabit fonksiyondur.
	s(A) = m, s(B) = n olmak üzere, A dan B ye n tane sabit fonksiyon tanımlanabilir.

6. Çift ve Tek Fonksiyon

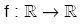
f(–x) = f(x) ise, f fonksiyonu çift fonksiyondur.

f(–x) = –f(x) ise, f fonksiyonu tek fonksiyondur.

	Çift fonksiyonların grafikleri Oy eksenine göre simetriktir.
	Tek fonksiyonların grafikleri orijine göre simetriktir.

 daha fazla bilgi için buraya tıklayınız