FONKSİYONLAR
FONKSİYON
A. TANIM
A ¹ Æ ve B ¹ Æ olmak üzere, A dan B ye bir b bağıntısı verilmiş olsun.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.
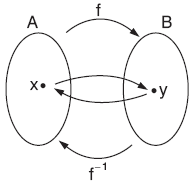
“x Î A ve y Î B olmak üzere, A dan B ye bir f fonksiyonu
f : A ® B ya da x ® f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye de değer kümesi denir.
f : A ® B ya da x ® f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye de değer kümesi denir.
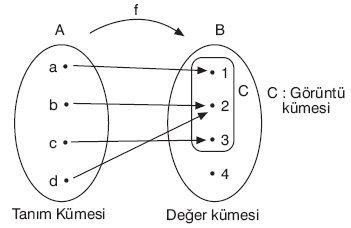
Yukarıda A dan B ye tanımlanan f fonksiyonu
f = {(a, 1), (b, 2), (c, 3), (d, 2)}
biçiminde de gösterilir.
| Ü | Her fonksiyon bir bağıntıdır. Fakat her bağıntı fonksiyon olmayabilir. |
| Ü | Görüntü kümesi değer kümesinin alt kümesidir. |
| Ü | s(A) = m ve s(B) = n olmak üzere,
i) A dan B ye nm tane fonksiyon tanımlanabilir.
ii) B den A ya mn tane fonksiyon tanımlanabilir.
iii) A dan B ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı 2m × n – nm dir.
|
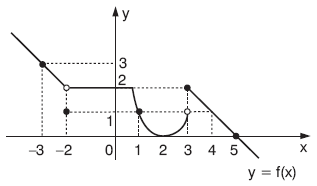
| Ü | Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği eğride en az bir ve en çok bir noktayı kesiyorsa verilen bağıntı x ten y ye bir fonksiyondur. |
B. FONKSİYONLARDA İŞLEMLER
A Ç B ¹ Æ olmak üzere,
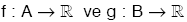 fonksiyonları tanımlansın.
fonksiyonları tanımlansın.- (f + g) : A Ç B ®
 , (f + g)(x) = f(x) + g(x)
, (f + g)(x) = f(x) + g(x) - (f – g) : A Ç B ®
 , (f – g)(x) = f(x) – g(x)
, (f – g)(x) = f(x) – g(x) - (f × g) : A Ç B ®
 , (f × g)(x) = f(x) × g(x)
, (f × g)(x) = f(x) × g(x) - “x Î A Ç B için, g(x) ¹ 0 olmak üzere,
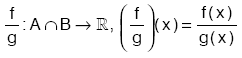
- c Î
 olmak üzere,(c × f) : A ®
olmak üzere,(c × f) : A ® , (c × f)(x) = c × f(x) tir.
, (c × f)(x) = c × f(x) tir.
daha fazla bilgi için tıklayınız
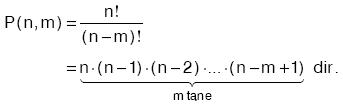
.png)



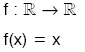
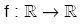
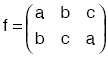 biçiminde gösterilir.
biçiminde gösterilir.