FOOPLOT
FooPlot is an online graphing calculator and function plotter. FooPlot is an open source application which you can access source code and you can modify it. You can draw a function using with this web based application.
FooPlot supports various functions as like below:
Trigonometric functions: sin(x), cos(x), tan(x), sec(x), csc(x), cot(x), asin(x), acos(x), atan(x), asec(x), acsc(x), acot(x)
Hyperbolic trigonometric functions:
sinh(x), cosh(x), tanh(x), sech(x), csch(x), coth(x), asinh(x), acosh(x), atanh(x), asech(x), acsch(x), acoth(x)
Miscellaneous:
ln(x), log(x), sqrt(x), abs(x), floor(x), ceil(x), u(x)
Min/Max:
min(expression1,expression2,expression3,...)
max(expression1,expression2,expression3,...)
Miscellaneous:
ln(x), log(x), sqrt(x), abs(x), floor(x), ceil(x), u(x)
Min/Max:
min(expression1,expression2,expression3,...)
max(expression1,expression2,expression3,...)
FooPlot has good properties. You can save your graph output as a PDF/EPS/PNG/SVG file. FooPlot supports π and e numbers. You can create a permalink for your graph and you can share this permalink if you want.
View of x^4-6x^3+7x^2+3x-4 graph:
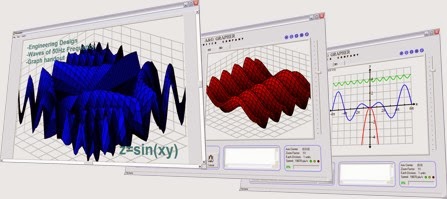
FooPlot looks like on you browser:
Using of FooPlot is very easy. You can write the function in text box at the right side. Then press enter key on you keyboard.
FooPlot can be used in schools, labs. It can be helpful for students, teachers. And you can use it at home for specific purposes.
One day, if you want to know that what the graph log(pi*x) + sec(60) looks like? Just then, you can visit FooPlot web site and you can see what the graph appearance.










.png)
.png)

.png)


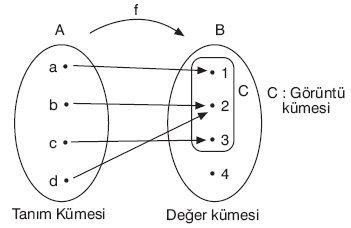
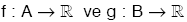 fonksiyonları tanımlansın.
fonksiyonları tanımlansın. , (f + g)(x) = f(x) + g(x)
, (f + g)(x) = f(x) + g(x)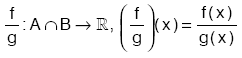
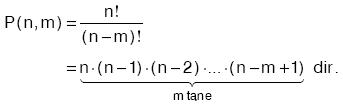
.png)



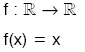
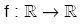
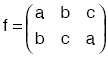 biçiminde gösterilir.
biçiminde gösterilir.